17.12.2016 Немного о системах координат в картографии
Введение
Если вы когда-либо держали в руках листы топографической карты (масштаба не мельче, чем 1:200000), то, возможно, обращали внимание на скромную надпись в левом верхнем углу листа «Система координат 1942 г.».
Дело в том, что почти все топографические карты крупного масштаба на территорию бывшего СССР выполнены именно в этой системе координат. Большинство тематических карт, в том числе и карт геологического содержания, также построены в системе координат 1942 года, поскольку основой для их создания были карты топографические.
Геологи и геофизики, работая в поле или составляя отчеты, из года в год используют хорошо знакомые им листы топографических и других карт. Однако мало кто из них сможет внятно объяснить, что такое система координат 1942 года. Может быть, им это и не нужно, если они всю жизнь работают только с бумажными картами. Но тому, кто желает работать c ГИС, разобраться в этом вопросе просто необходимо.
Картографическая система координат 1942 года (СК-42) представляет собой систему плоских прямоугольных координат. Она основана на проекции Гаусса-Крюгера, которая была предложена еще в первой половине XIX в. и используется до сих пор. Часто СК-42 и проекцию Гаусса-Крюгера отождествляют, хотя, строго говоря, это не одно и то же.
Процесс переноса реальной земной поверхности на плоскость карты представляет собой довольно сложный и витиеватый путь, который выполняется в несколько шагов:
- Нерегулярная форма Земли (геоид) аппроксимируется некоторой регулярной поверхностью (то есть такой, которую можно описать одной формулой).
- Выбранная поверхность фиксируется относительно тела Земли и становится поверхностью относимости (называемой также референцповерхностью). Этим задается система геодезических (географических) координат.
- Поверхность относимости масштабируется (уменьшается) соответственно главному масштабу карты.
- Изображение географических объектов с уменьшенной поверхности относимости строгими математическими методами отображается (проецируется) на плоскость или развертываемую без искажений поверхность.
Рассмотрим все эти шаги по очереди.
1. Некоторые понятия теории фигуры Земли
В теории фигуры Земли используется понятие об уровенной поверхности [2], которая определяется как непрерывная поверхность во всех точках нормальная направлению отвесных линий (направлению силы тяжести).
Очевидно, мысленно можно представить бесчисленное множество уровенных поверхностей, огибающих Землю. Поверхность Мирового океана, находящаяся в состоянии покоя тоже является уровенной поверхностью. Она называется средней уровенной поверхностью, или поверхностью геоида.
Поверхность геоида не является стабильной и, претерпевая непрерывные изменения во времени, может быть зафиксирована только для определенного момента. Изменения поверхности (колебания уровня Мирового океана и суши) обусловлено лунно-солнечным притяжением, вызывающие морские приливы, и различными геологическими и метеорологическими факторами, математическое описание которых затруднено, а зачастую и невозможно. Поэтому фиксация поверхности геоида может быть произведена только приближенно, на основании результатов длительного наблюдения уровня океана. В России в качестве начальной точки, лежащей на поверхности геоида, принят нуль Кронштадского футштока, фиксирующий средний уровень Балтийского моря.
Использование геоида как характеристики фигуры Земли затруднено еще и тем, что для изучения поверхности геоида недостаточно знать гравитационное поле Земли, а необходимо привлекать данные о распределении по плотности масс Земной коры. Строение Земной коры изучено еще недостаточно полно, и это делает невозможным точное определение поверхности геоида и вынуждает решать эту задачу приближенно, прибегая к тем или иным гипотезам и предположениям.
В настоящее время для исследования фигуры Земли, а также для решения геодезических задач используется так называемый квазигеоид (рис.1). Преимущество квазигеода состоит в том, что его поверхность может быть изучена только на основании гравиметрических данных, без привлечения данных о структуре Земной коры.
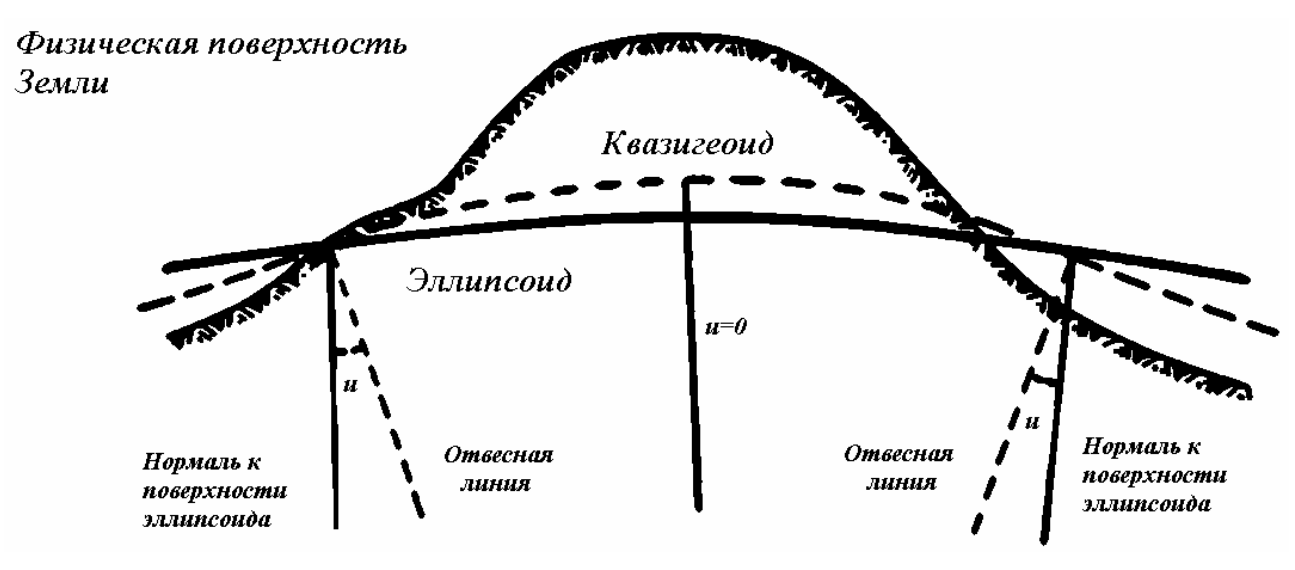
Поверхности геоида и квазигеоида совпадают на территории Мирового океана, на равнинах различаются не более чем на несколько см, в горных районах – различие достигает 2 м (рис.1).
Поверхности геоида и квазигеоида не являются математически правильными неизменными во времени и поэтому для обработки геодезических измерений нужно использовать стабильную и более простую поверхность сравнения. В картографии в качестве таковой используют поверхность эллипсоида вращения.
Здесь мы вынуждены сделать небольшое отступление от общего повествования для тех, кто не имеет понятия об эллипсоидах вращения и о том, каким образом они могут представлять поверхность Земли.
1.1. Понятие об эллипсоиде вращения.
Подобно тому, как сфера основана на круге, эллипсоид основан на эллипсе. В общем случае рассматривают трехосный эллипсоид. В зависимости от соотношения длин его осей возможно три случая: сфера (все три оси равны), эллипсоид вращения (две оси равны), трехосный эллипсоид (все оси - разные).
Сфера используется только для мелко масштабных карт (мельче 1:1000000). При этих масштабах невозможно заметить на карте разницу между сферой и эллипсоидом. Однако для поддержки точности карт более крупного масштаба Землю следует рассматривать как эллипсоид.
Трехосный эллипсоид используется практически только для представления небесных тел неправильной формы. Для представления земной поверхности в ГИС он не актуален, а используется только в особо точных геодезических измерениях.
Для построения топографических карт в большинстве случаев выбирают эллипсоид вращения. Так же, как вращение круга вокруг оси, определяемой его диаметром, образует сферу, вращение эллипса вокруг его большой или малой оси образует эллипсоид.
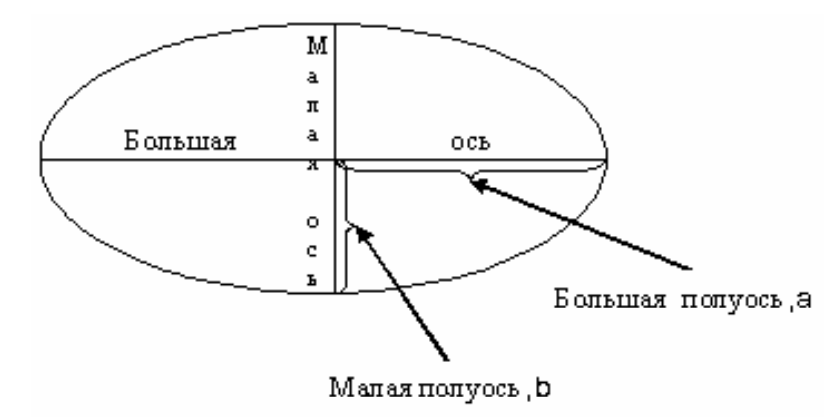
Эллипс задается двумя параметрами - длинами двух полуосей a и b (рис.2), или (более распространенный случай) длиной большой полуоси а и коэффициентом сжатия f = (a-b)/a. Значения сжатия находятся в диапазоне от 0 до 1. Сжатие 0 означает, что обе оси равны, т.е. мы имеем дело с кругом.
Сжатие 1 означает фигуру только с одной осью, выглядящую как отрезок прямой, длина которого равна длине большой оси. В общем случае большие значения сжатия описывают узкие эллипсы, а малые значения сжатия описывают почти круглые эллипсы.
Эллипсоид, который почти напоминает сферу, называется «сфероид» (рис.3). Эллипсоид, почти напоминающий форму Земли, образован вращением вокруг малой оси.

Эллиптичность сферы равна 0, в то время как эллиптичность Земли составляет примерно 0.003353.
Явление сжатия наблюдается на полюсах, расширение происходит на экваторе. Поэтому большая полуось описывает экваториальный радиус, а малая полуось представляет полярный радиус.
Размеры эллипсоида и его ориентировка в теле Земли должны быть такими, чтобы поверхности эллипсоид и квазигеоида были по возможности близки друг другу. Наилучшим образом этому удовлетворяет общеземной эллипсоид (World ellipsoid), у которого:
- центр совпадает с центром тяжести Земли, а плоскость экватора совпадает с плоскостью земного экватора
- сумма квадратов отклонений по высоте поверхности эллипсоида от поверхности квазигеоида - минимальная.
В настоящее время задачи определения параметров общеземного эллипсоида решаются путем проведения измерений с помощью спутниковых геодезических систем. Использование спутниковых технологий позволило обнаружить несколько эллиптических отклонений: например, южный полюс находится ближе к экватору, чем северный полюс. Общеземной эллипсоид аппроксимирует поверхность Земли в целом. В США в настоящий момент используется общеземной эллипсоид WGS-84 (World Geodetic System 1984), в России – ПЗ-90 (Параметры Земли 1990 г.). Задачи определения размеров общеземного эллипсоида и его ориентирования в теле Земли должны решаться совместно. Однако точное выполнение указанных выше условий невозможно без детальной изученности поверхности квазигеоида в целом.
До создания спутниковых геодезических систем параметры эллипсоидов определялись в результате вычислительной обработки данных государственных и региональных геодезических сетей. При этом задача установления эллипсоида обычно разбивается на две части:первоначально, используя результаты геодезических и гравиметрических работ, определяют размеры эллипсоида, а затем ориентируют эллипсоид в Земле. Полученный таким способом эллипсоид называется референц-эллипсоид.
Поскольку геодезические сети создавались на разных континентах, разными средствами и с разным уровнем точности, на настоящий момент имеется более двух десятков референц-эллипсоидов, каждый из которых оптимален лишь для определенной части Земли. Для территории России таким эллипсоидом является эллипсоид Красовского, рассчитанный в 1940 г.
Таким образом эллипсоиды бывают 2 типов: общеземные, аппроксимирующие поверхность Земли в целом и референцэллипсоиды, наиболее точно представляющие поверхность Земли на некоторой ограниченной территории, например, в пределах отдельной страны.
Следует отметить, что в справочных расчетах сфероиды, определенные с помощью спутниковых технологий, начинают вытеснять сфероиды, определенные в результате наземных измерений. Фактом, который необходимо учитывать перед тем, как внести изменения в справочный сфероид, является воздействие такого изменения на все предварительно измеренные величины. Из-за сложности измерения сфероидов те из них, которые были получены в результате наземных измерений, все еще используются и все еще представляют собой ценный справочный материал. Названия некоторых сфероидов, размеры осей и географические местоположения, к которым они могут применяться перечислены в таблице 1 [5]. Вы заметите, что значения действительно варьируют, но лишь в небольших размерах по отношению к размерам Земли.
| Название | Дата (год) | Большая полуось, (м) | Малая полуось, (м) | Использование |
|---|---|---|---|---|
| Эйри | 1830 | 6377563.396 | 6356256.91 | Великобритания |
| Австралийская национальная | 6378160 | 6356774.719 | Австралия | |
| Бессель | 1841 | 6377397.155 | 6356078.963 | Большинство областей Центральной Европы, Чили |
| Кларк | 1866 | 6378206.4 | 6356583.8 | Североамериканский континент и Филиппины |
| Кларк | 1880 | 6378249.145 | 6356514.86955 | Франция и большая часть Африки |
| Эверест | 1830 | 6377276.3452 | 6356075.4133 | Индия, Бирма, Цейлон, Малайзия |
| СР380 | 1980 | 6378137 | 6356752.31414 | Северная Америка |
| Хельмерт | 1907 | 6378200 | 6356818.17 | Египет |
| Красовский | 1940 | 6378245 | 6356863.0188 | СССР и некоторые страны Восточной Европы |
| WGS84 | 1984 | 6378137 | 63565752.31 | Во всем мире |
2. Система геодезических координат (DATUM).
Следующим этапом является задание системы геодезических координат на поверхности эллипсоида. В качестве координат используются криволинейные координаты, известные как широта и долгота. Хотя начало координат определяется как точка на пересечении экватора и Гринвичского меридиана, в действительности для задания отсчета координат используется косвенный метод, когда для некоторой точки на реальной поверхности Земли (так называемого начального пункта) фиксируются значения широты и долготы, производится совмещение нормали к поверхности референц-эллипсоида и отвесной линии в данной точке, а плоскость меридиана исходного пункта устанавливается параллельно оси вращения Земли. Эти исходные данные, называемые также геодезическими датами (datum), жестко фиксируют систему геодезических координат относительно тела Земли. Для эллипсоида Красовского такая точка задана в Пулково (центр круглого зала обсерватории), и этим задается основа Системы координат 1942 г. (СК-42).
3. Главный и относительный масштабы.
Упрощенно процесс проецирования можно представить 2 этапами: в начале преобразуем Земной шар в промежуточный сфероид в зависимости от выбранного масштаба, затем этот сфероид проецируется на плоскую поверхность. Численный масштаб первого преобразования называется главным масштабом: он равен отношению радиуса промежуточного сфероида к радиусу Земли.
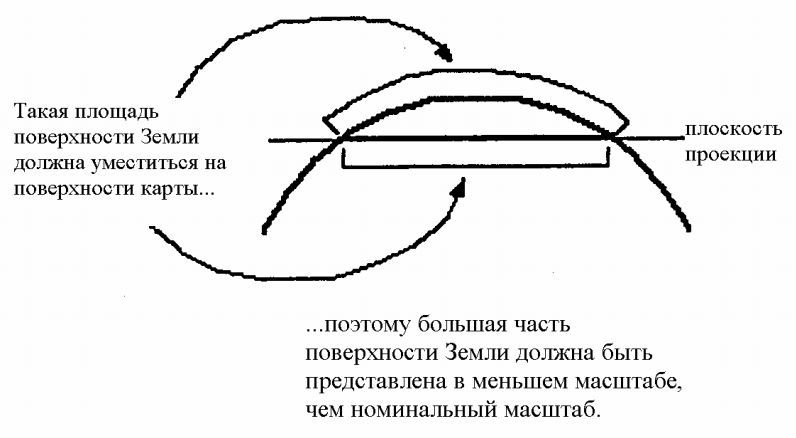
Теперь рассмотрим еще одно новое понятие - масштабный коэффициент [4]. Масштабный коэффициент, называемый также относительным масштабом, определяется как отношение местного масштаба на карте к главному масштабу. По определению масштабный коэффициент на промежуточном сфероиде равен 1. Когда же мы переходим от его сферической поверхности к двумерной карте местный масштаб не будет равен главному, поскольку плоская и сферическая поверхности не совместимы (рис.4). Следовательно, масштабный коэффициент в общем случае не равен 1 и будет различным в разных частях карты. Чем больше масштабный коэффициент отличен от 1, тем сильнее искажения на карте.
4. Картографические проекции.
Глобус – традиционный способ отображения формы Земли. Хотя глобусы в целом передают форму Земли и показывают пространственные очертания объектов размером с континент, на практике они не применяются. Глобус даже очень мелкого масштаба (1:1000000000) будет очень велик, так что его в карман не сунешь и полевую сумку не положишь. На практике, для проведения полевых работ и анализа полученных данных мы используем значительно более крупные масштабы, где-то от 1:1000000 до 1:5000, в зависимости от уровня детализации. Сделать глобус такого масштаба придет в голову разве что чудаку-гигантоману. Поэтому картографы разработали набор методов, называемых картографическими проекциями, которые предназначены для изображения с приемлемой точностью сферической Земли на плоском носителе.
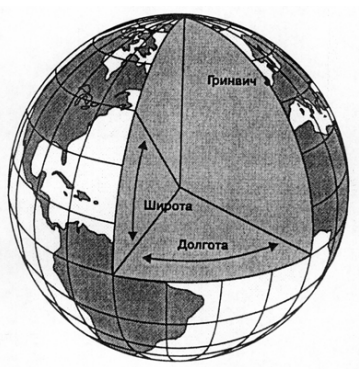
Есть еще одна причина, которая вынуждает нас применять на практике плоские карты. На глобусе достаточно легко определить местоположение объекта, зная его сферические координаты: широту и долготу (рис.5). Однако в большинстве случаев нам недостаточно просто знать, где расположен объект. Нам интересно знать, как он взаимодействует с другими объектами, а для этого нужно проводить измерения: расстояний, длин, площадей, направлений, и т.д. Для проведения измерений сферические координаты приспособлены плохо. Основная причина заключается в том, что угловому расстоянию в 1 градус на разных широтах соответствует неодинаковое линейное расстояние на поверхности Земли: если 1 градус на экваторе (или любой другой линии большого круга 1) составляет ≈111 км, то на широте отличной от 00 эта величина будет меньше. Т.е. расстояние на поверхности Земли, соответствующее 1 градусу углового расстояния, вообще говоря, является величиной переменной, зависящей от значения широты. Использование прямоугольных систем координат освобождает нас от подобных проблем.
Физически процесс создания проекций можно уподобить проецированию лучей источника света из центра сфероида на поверхность проекции (рис.6).
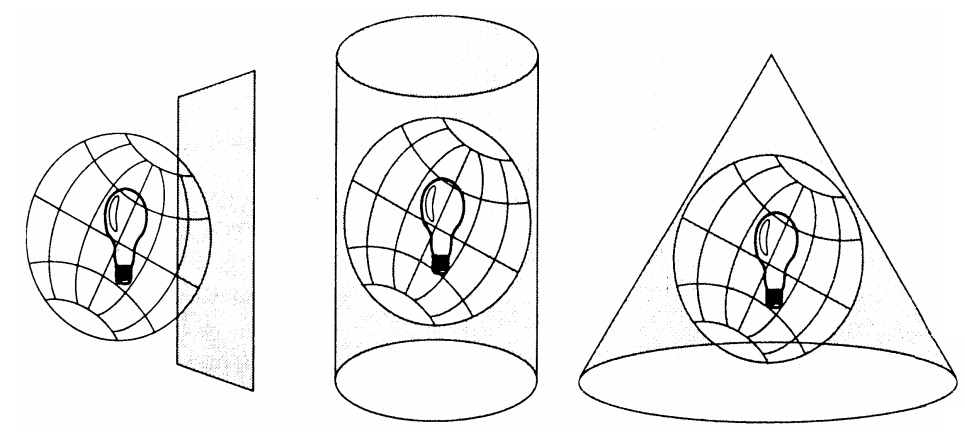
Фигура для проецирования выбирается такой, чтобы ее можно было развернуть в плоскость без растяжения их поверхностей. Обычными примерами форм, удовлетворяющих этому критерию, являются конусы, цилиндры, плоскости. В зависимости от выбора фигуры для проецирования, различают 3 семейства картографических проекций: конические, цилиндрические, планарные [5].
Первым шагом при построении проекции одной поверхности на другую является создание одной или более точек контакта. Каждая такая точка называется точкой касания. Плоскостная проекция проходит по касательной к глобусу только в одной точке. Касательные конусы и цилиндры вступают в контакт с глобусом вдоль линии. Если поверхность проекции пересекает глобус вместо того, чтобы просто коснуться его поверхности, полученная в результате проекция концептуально требует вычисления секущей, а не касательной линии. Независимо от того является ли контакт касательным или секущим, его место очень значимо, поскольку определяет точку или линии нулевого искажения. Эту линию истинного масштаба часто называют стандартной линией. В общем, искажение увеличивается с увеличением расстояния от точки контакта.
Проекции – не абсолютно точные представления географического пространства. Каждая создает свой набор типов и величин искажений на карте. Бывают искажения формы (или углов), площади, расстояния и направления. Для представления различных частей земной поверхности используют разные разновидности картографических проекций. Некоторые картографические проекции сводят к минимуму искажения по одному параметру за счет увеличения искажения по другим параметрам, в то время как другие проекции пытаются минимизировать все искажения в равной степени [4].
На рисунке 7 показаны некоторые виды проекций [5]. Вообще существует сотни видов и разновидностей проекций. Но для нас интересными будут цилиндрические проекции, поскольку проекция Гаусса-Крюгера является поперечно-цилиндрической проекцией.
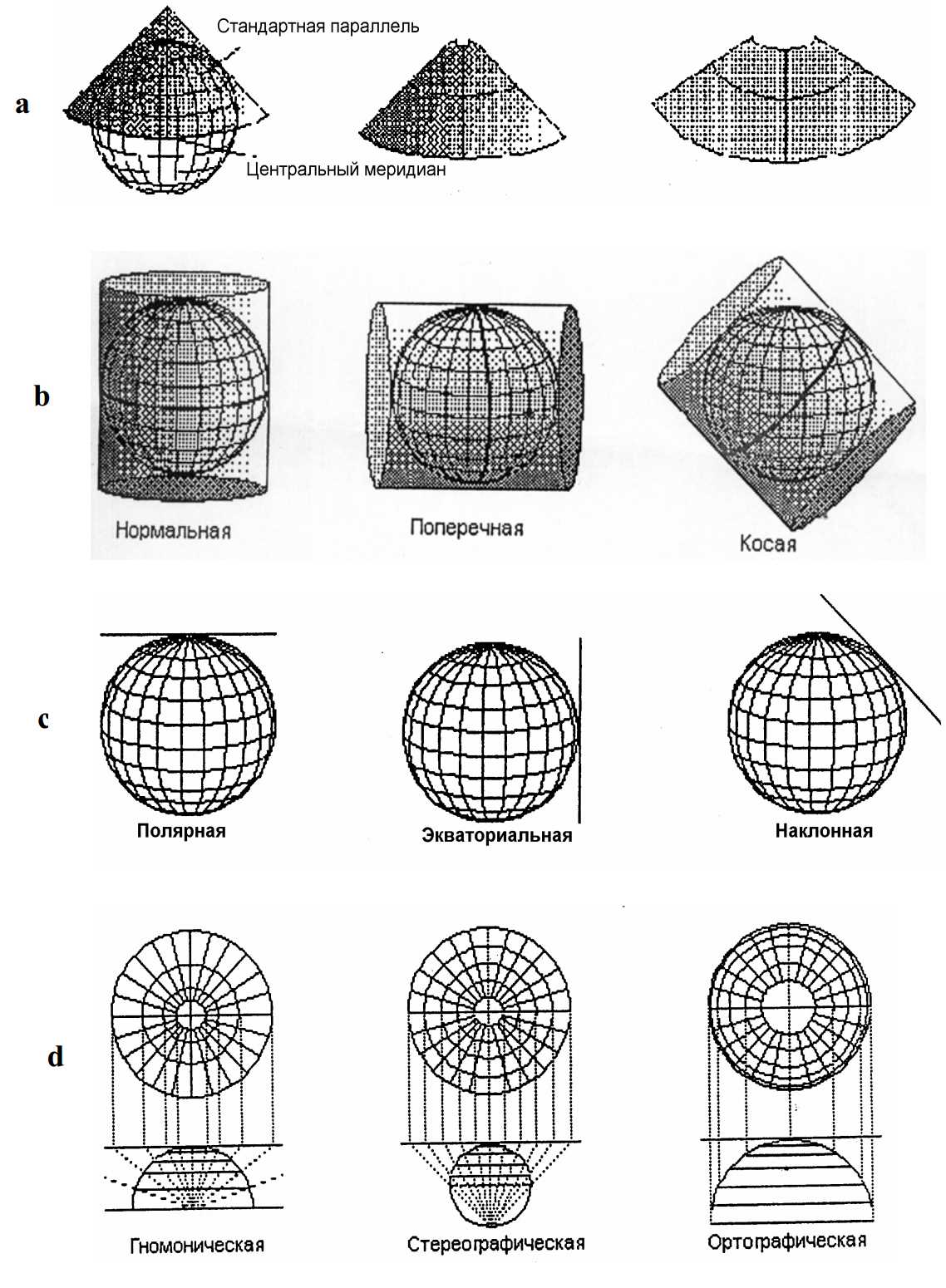
Цилиндрические проекции могут иметь одну линию касания или две линии сечения на глобусе. Экватор обычно является линией касания. Меридианы проецируются геометрически на цилиндрическую поверхность, а параллели проецируются математически, создавая углы 90° координатной сетки. Цилиндр можно «рассечь» вдоль меридиана для получения конечной цилиндрической проекции (рис.8). Меридианы расположены через равные интервалы, в то время как интервал между параллельными линиями широты возрастает по направлению к полюсам.
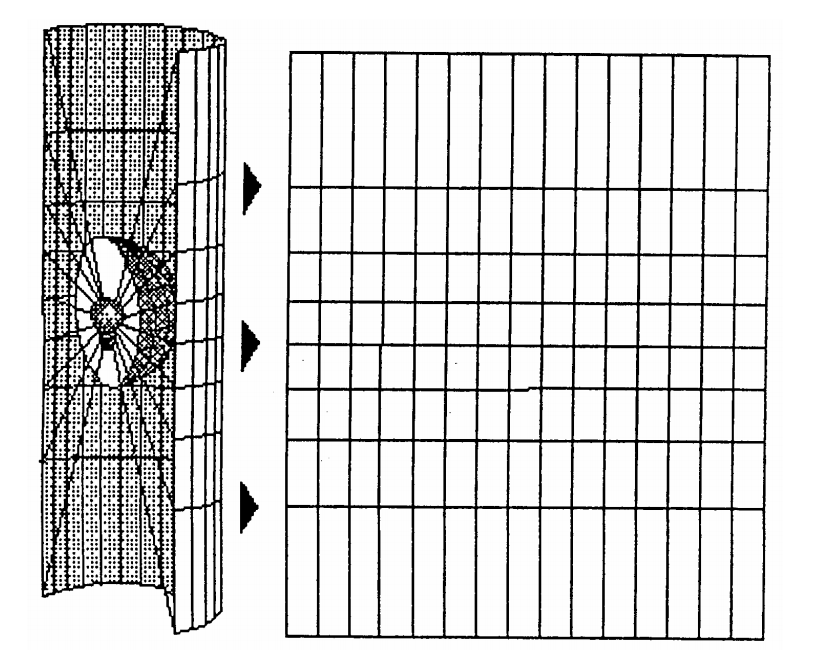
Эта проекция является равноугольной и показывает истинное направление вдоль прямых линий.
При создании более сложных цилиндрических проекций цилиндр вращают, таким образом изменяя линии касания или сечения. Поперечные цилиндрические проекции, такие как Поперечная проекция Меркатора или Гаусса-Крюгера, используют меридианы как линии касательного контакта, так что ось цилиндра лежит в плоскости экватора. Линии касания идут на север и юг, и вдоль них масштаб является истинным.
Теперь, когда основные этапы получения картографических проекций рассмотрены и необходимые для их понимания характеристики карт определены, можно дать развернутое, подробное описание системы координат СК-42.
5. СК-42.
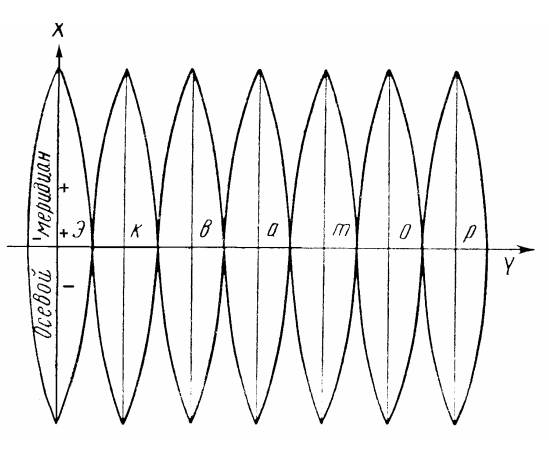
СК-42 можно охарактеризовать как прямоугольные координаты в зональной системе. Под зональной системой в данном случае подразумевается проекция Гаусса-Крюгера. Она делит Земную поверхность на 60 пронумерованных зон шириной по 6 градусов долготы каждая (рис.9). Значения крайних меридианов шестиградусных зон будут иметь значения: первая зона 0—6°, вторая зона 6—12°, третья зона 12—18° и т. д. Следует сразу отметить, что положение зон в проекции Гаусса - Крюгера совпадает с положением зон международной системы разграфки земной поверхности на шестиградусные зоны (рис.10), называемые (по международному соглашению) колоннам, но отличается по номеру. Поскольку нумерация колонн идет не от 0° меридиана, а от 180°, то номер зоны будет отличаться от номера колонны на 30, т.е.: n = N-30, где n — номер шестиградусной координатной зоны, а N — номер колонны листов карты масштаба 1 : 1 000 000 [2].
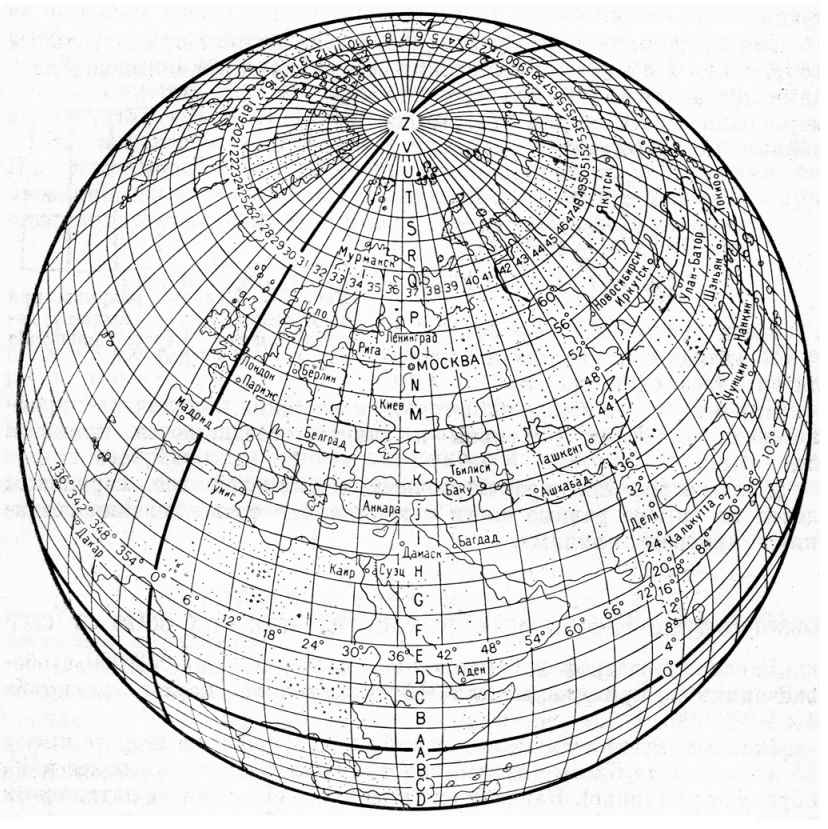
Территория России размещена в зонах с 4 по 32. По номеру зоны можно определить долготу осевого и крайних граничащих меридианов. Так, например, в четвертой зоне крайний западный меридиан равен 18°, восточный 24°, а осевой 21°.
Зональная проекция подразумевает проведение проецирования не одновременно для всего сфероида, а отдельно для каждой зоны. Проецирование осуществляется столько раз, сколько существует зон. Для получения проекции какой-либо из 60-ти зон, цилиндр размещают относительно сфероида таким образом, чтобы поверхность цилиндра наиболее плотно прилегала к поверхности сфероида в пределах этой зоны. Такой способ проецирования позволяет свести искажения, неизбежные при проецировании, к минимуму. Проекция Гаусса-Крюгера является конформной (равноугольной), искажения площадей, расстояний и направлений в пределах каждой зоны минимальны: вдоль осевого меридиана искажения отсутствуют, следовательно, масштабный коэффициент вдоль осевого меридиана сохраняется и равен 1. При удалении от осевого меридиана искажения становятся отличными от 0 и достигают своего максимального значения равного 1/750 на границе зоны.
По широте зона проходит от полюса до полюса. Меридианы и параллели представляют собой кривые линии, за исключением осевого меридиана. Как было указано выше, каждая зона представляет особую координатную систему. Начало координат каждой зоны находится в точке пересечения кватора со средним (осевым) меридианом зоны. Система координат прямоугольная. Каждая зона имеет свое начало координат. Осевой меридиан и экватор принимают за координатные оси (рис.11): осевой меридиан за ось абсцисс, а экватор за ось ординат. Единица измерения – метр.
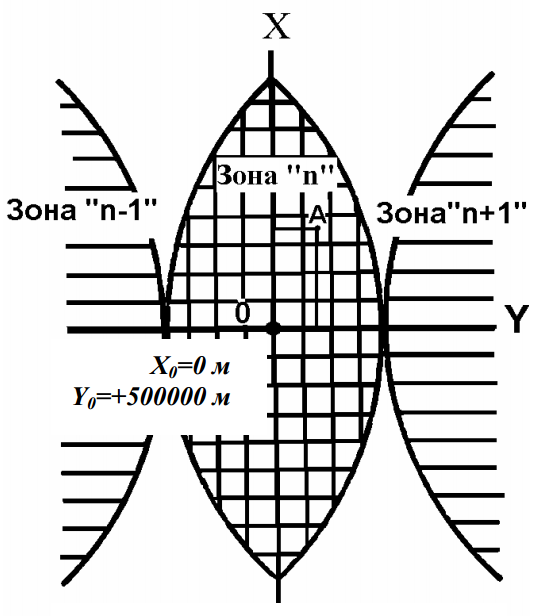
Если меридиан разделить на равные отрезки и через точки деления провести вертикали, а на земной поверхности провести малые круги на тех же расстояниях друг от друга и все это спроектировать на плоскость, соблюдая условие равноугольности, то на плоскости окажется сетка практически равных квадратов. Линии, образующие стороны этих квадратов, называются километровыми и проводятся на картах обычно на расстоянии целых километров друг от друга. Линии одной системы параллельны среднему меридиану зоны, а линии другой системы параллельны экватору. Километровые линии вычерчиваются на всех топографических картах и служат для определения прямоугольных координат точек и для решения других задач по карте.
Вся территория бывшего СССР расположена в северном полушарии, поэтому абсциссы всех ее точек будут положительны 1.
Чтобы не иметь дела с отрицательными ординатами, условно принимают ординату точки О, т. е. начала координат, равной 500 км (рис.11), или, иначе, увеличивают значения ординат на 500 км. При этом условии даже на экваторе самая западная точка зоны будет иметь ординату примерно +165 км. Такой прием является общепринятым, и используется при определении многих систем координат (например, UTM). Это смещение называют ложным сдвигом в восточном направлении.
Положим, что две точки определены их координатами [3]: xА = 5 973 км, yА = 722 км и xB = 973 км, yB = 395 км
Это значит, что расстояние до обеих точек от экватора равно 5 973 км и что точка A лежит в зоне на восток от осевого меридиана в расстоянии 222 км, а точка B на запад — 105 км.
Территория России располагается в 28 зонах. Значит, точек с такими координатами в пределах нашей страны будет тоже 28. Чтобы точно указать, о какой точке из 28-ми идет речь, надо указать еще номер зоны, например, 7. Номер зоны вводится и ординату. Ордината получит вид: yА = 7 722; yB = 7 395.
Если дано у = 13 642, значит, точка лежит в 13-й зоне, а условная (увеличенная на 500 км) ордината ее 642 км.
Как было сказано выше, на каждой топографической карте можно видеть километровые квадраты (на картах масштаба 1:100000 — двухкилометровые), причем километровые линии имеют подписи целых чисел километров от соответствующих осей.
Километровая разграфка для листов N—37—133—В, N—37—144—Г масштаба 1:50000 показа на рисунке 12.
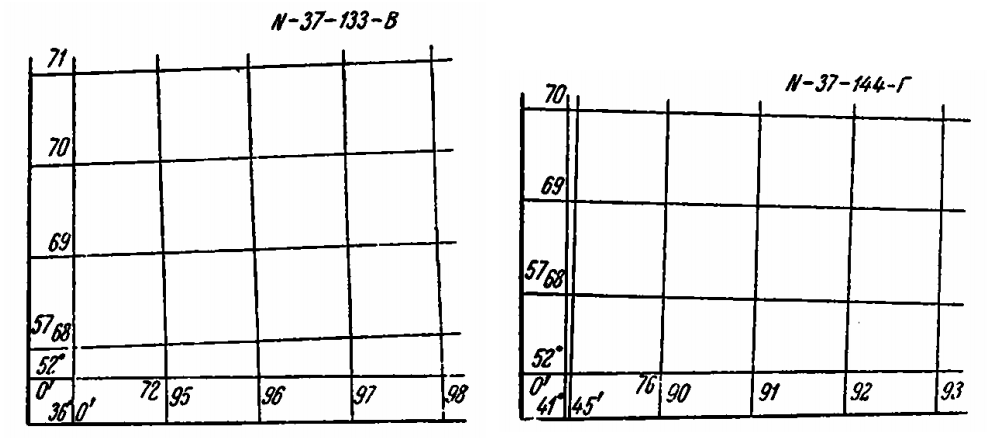
Самая южная линия на карте, перпендикулярная осевому меридиану, имеет подпись числа километров до этой линии от экватора по осевому меридиану — 5768. Другие, параллельные ей, проведенные через 1 км, подписаны числом десятков и единиц километров, т. е. 69, 70, 71 и т. д. Первые две цифры значения абсцисс не повторяются, а пишутся только последние две цифры. Полностью абсциссы подписываются только в верхнем и нижнем углах трапеции.
Также полностью подписываются ординаты только крайних линий, как, например, 7295 на листе К—37—133— В и 7690 на листе К—-37—144—Г. Остальные ординаты сохраняют только две последние цифры—соответственно, 96, 97, 98 и т. д. и 91, 92 и т. д. Первая в ординате цифра 7 означает номер зоны.
6. СК-42 и другие вопросы геопривязки.
Когда мы имеем дело с электронными картами или используем в своей работе данные дистанционного зондирования, практически, всегда возникает необходимость их географической привязки. Хотя сам по себе этот процесс не сложен, в нем есть подводные камни, о которых нужно знать. Пока рабочие материалы остаются в пределах одной системы координат или проекции, например, СК-42 – все просто. Но при переходе к данным другого масштаба, смене проекции, объединении в одном проекте данных из разных источников, переходе от местных координат к глобальным эти проблемы дают о себе знать: изображения объектов в одних слоях оказываются смещены относительно тех же объектов в других слоях. Виной тому могут быть и объективные обстоятельства и ошибки пользователя.
Большинство пользователей ГИС, не имеющих геодезического образования, полагают, что широта и долгота любой точки на поверхности Земли – есть величина абсолютная, ни от чего не зависящая. Увы, это не так. Если задать, для входных данных и результата одну и ту же проекцию Geographic (Lat/Lon), но разные эллипсоиды (например, Красовского и WGS-84), то вы увидите, что значения широты и долготы одной и той же точки на двух эллипсоидах будут разными. Следовательно, для того, чтобы свести все данные к одной системе координат или проекции, необходимо совершенно точно знать все параметры входной и выходной проекции. При этом следует помнить, что процесс проецирования и перепроецирования исходных данных представляет собой довольно громоздкий пересчет, в результате которого могут накопиться ошибки. Эти ошибки обусловлены ошибками округления компьютера и недостатками вычислительных алгоритмов.
Часто возникает проблема, когда изучаемая область пересекает две или более зон, т.к. географические границы часто не соответствуют структуре зон. Если ваша изучаемая область занимает более одной зоны, вы имеете несколько возможностей для выбора. Например:
- Определите, какую зону занимает большая часть изучаемой области (например, 9 зону). Затем в систему координат 9-ой зоны включите область, оставшуюся вне данной зоны. Такой подход может дать неожиданный эффект, потому что вы используете стандартные параллели 9 зоны, чтобы проектировать другую зону. Как результат, объекты другой зоны могут исказиться (другими словами, сместиться) на несколько сотен метров.
- Откажитесь от СК-42; выберите другую проекцию. Возможно, ваша новая проекция и координатная система избежит таких проблем.
- Создайте вашу собственную проекцию. Она может устраивать вас на данный момент, но дальше могут возникнуть проблемы, потому что никто не будет знать, какой проекцией вы пользовались. Проблемы могут возникнуть из-за того, что вы по незнанию можете дать или получить данные в различных системах координат.
- Храните все в десятичных градусах и проектируйте, когда возникает потребность.
Перевод карты или изображения из одной проекции в другую обычно выполняется в два или три шага. На первом шаге координаты исходной проекции пересчитываются в географические – широту и долготу. То есть, решается обратная задача проецирования. Если исходная и целевая проекции используют один и тот же референцэллипсоид, то вторым шагом будет пересчет полученных географических координат в координаты целевой проекции, то есть, – обычное прямое проецирование. Очень просто: из одной проекции – на эллипсоид, и далее – в другую проекцию. Программное обеспечение фирм ESRI и ERDAS при отображении и анализе данных может выполнять прямое проецирование "на лету". Поэтому очевидно, что хранить данные чаще всего имеет смысл не в плоских координатах проекции (километровых), а в угловых географических. Тогда при смене проекции не будет выполняться первый шаг – обратное проецирование, – который неизбежно снижает точность данных из-за ограниченной точности представления чисел в компьютере и ошибок округления при вычислениях (часто главным фактором является представление обратной проекции с помощью полиномов из-за невозможности получения точной формулы). С другой стороны, проецирование "на лету" требует выполнения соответствующих вычислений, что, конечно же, снижает скорость отображения. И если совершенно точно известно, что проекция меняться не будет, то данные имеет смысл хранить проецированными. Если же есть возможность хранить и проецированные, и непроецированные данные, то лучше ею воспользоваться. Если исходная и целевая проекции используют разные референц-эллипсоиды или геодезические даты, то на втором шаге будет выполнен пересчет горизонтальных географических координат с одного эллипсоида на другой, а пересчет в целевую проекцию будет третьим шагом.
От эллипсоидальных координат легко можно перейти к трехмерной прямоугольной системе координат с началом отсчета в центре эллипсоида (геоцентрическая система координат), и тогда переход от одного эллипсоида к другому будет определяться связью геоцентрических систем координат этих двух эллипсоидов (рис.13). В общем случае такая связь может быть выражена семью параметрами связи – сдвигами начала коодинат вдоль каждой оси (три линейных параметра), поворотами вокруг каждой оси (три угловых параметра) и одним масштабным коэффициентом. В целом, это преобразование осуществляется по формулам Хелмерта (Гельмерта). Поскольку повороты и масштабирование нужны не всегда, иногда используется более простое преобразование по трем параметрам. В некоторых случаях для преобразования эллипсоидов используются более сложные уравнения многомерной регрессии.
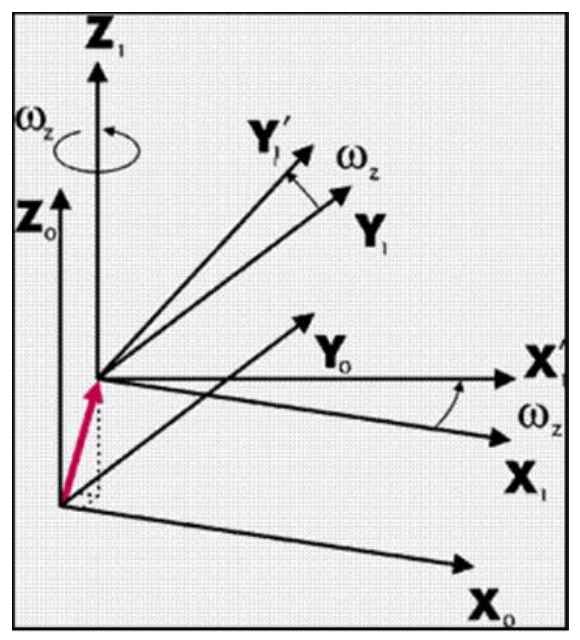
При использовании различных эллипсоидов следует иметь в виду, что в настоящий момент точные и однозначные параметры связи имеются не для всех комбинаций эллипсоидов. Так, например, параметры связи СК-42 и ПЗ-90 известны точно. В то же время известно несколько вариантов параметров связи ПЗ-90 и WGS-84. Причем смещение объектов на поверхности Земли при использовании разных вариантов может достигать сотен метров, что для крупного масштаба недопустимо. До опубликования официальных значений параметров связи, решением этой проблемы может быть использование только одного, известного варианта. Приобретая данные из разных источников, необходимо получать вместе с ними также и параметры связи, использованные для перехода из СК-42 на WGS-84, если такое преобразование имело место. И именно эти параметры связи должны закладываться в программное обеспечение для получения корректных результатов.
В заключение следует упомянуть о Постановлении Правительства РФ от 28.07.2000 N 568 "Об установлении единых государственных систем координат" [1]. Согласно ему все новые топогеодезические и картографические материалы и работы должны выполняться в Системе координат 1995 г. (СК-95) на эллипсоиде ПЗ-90. Это постановление вызвало ощутимую негативную реакцию со стороны географической общественности. Здесь же отметим, что для современных ГИС использование любой системы координат не представляет проблемы, если известны параметры ее связи с другими распространенными системами координат. Если же эти параметры не будут точно известны, то это только прибавит головной боли всем пользователям ГИС.
Литература
1. Андрианов В. Координаты пространственных данных. «ArcReview. Современные геоинформационные системы”. №2(17). М., изд-во Дата+, 2001.
2. Гараевская Л.С. Картография. М., изд-во «Недра», 1971.
3. Дензин П.В. Геодезия. М., изд-во Московского университета, 1953.
4. ДеМерс М. Географические информационные системы. Основы. М., изд-во Дата+, 1999.
5. Картографические проекции. Географическая привязка пространственных данных. М., изд-во Дата+, 1994.
Составитель: Ст. преподаватель Чернова И.Ю.